Laurentvidal.fr est la solution idéale pour ceux qui recherchent des réponses rapides et précises à leurs questions. Rejoignez notre plateforme pour vous connecter avec des experts prêts à fournir des réponses détaillées à vos questions dans divers domaines. Trouvez des solutions détaillées à vos questions grâce à une large gamme d'experts sur notre plateforme conviviale de questions-réponses.
Sagot :
Bonjour,
1) Pour la face avant du paquet, nous utilisons une longueur de ficelle égale à 2x.
Pour la face arrière du paquet, nous utilisons une longueur de ficelle égale à 2x.
Pour chaque face latérale, nous utilisons une longueur de ficelle égale x+y, soit 4(x+y) pour les 4 rectangles latéraux.
Au total, nous utilisons une longueur égale à 2x+2x+4(x+y) = 2x+2x+4x+4y.= 8x+4y.
Puisqu'il y a 100 cm de ficelle, nous avons : 8x + 4y = 100
2) 8x + 4y = 100 ===> 2x + y = 25
===> y = 25-2x.
Or y ≥ 0 ===> 25-2x ≥ 0
===> -2x ≥ -25
===> x ≤ (-25)/(-2)
===> x ≤ 12,5.
Comme x ≥ 0, nous déduisons que : 0 ≤ x ≤ 12,5
Df = [0 ; 12,5]
Le volume d'un parallélépipède rectangle est donné par : Aire de la base * hauteur.
Prenons le carré comme base. Son aire est égale à x*x = x².
La hauteur est alors égale à y.
D'où, f(x) = x²y
Or y = 25-2x. (voir ci-dessus)
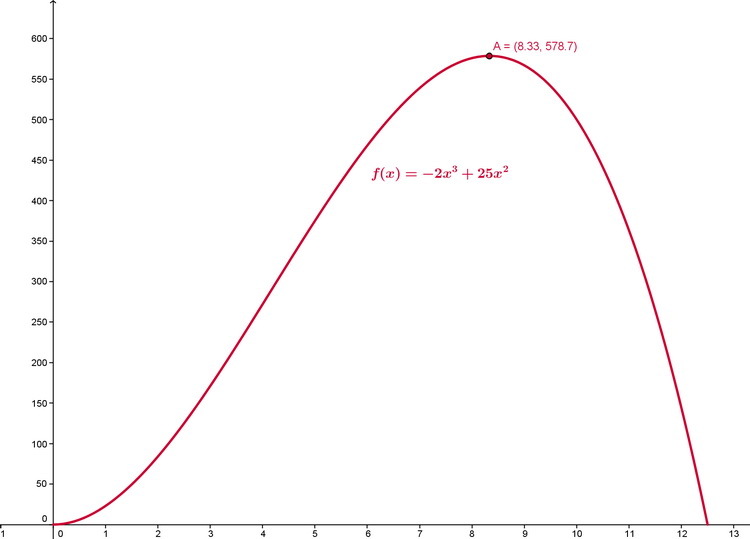
Donc [tex]f(x)=x^2(25-2x)[/tex] ou encore [tex]f(x)=25x^2 - 2x^3 [/tex]
3) Le graphique montre que f est maximal pour x ≈ 8,3 (cm)
(Graphique en pièce jointe)
1) Pour la face avant du paquet, nous utilisons une longueur de ficelle égale à 2x.
Pour la face arrière du paquet, nous utilisons une longueur de ficelle égale à 2x.
Pour chaque face latérale, nous utilisons une longueur de ficelle égale x+y, soit 4(x+y) pour les 4 rectangles latéraux.
Au total, nous utilisons une longueur égale à 2x+2x+4(x+y) = 2x+2x+4x+4y.= 8x+4y.
Puisqu'il y a 100 cm de ficelle, nous avons : 8x + 4y = 100
2) 8x + 4y = 100 ===> 2x + y = 25
===> y = 25-2x.
Or y ≥ 0 ===> 25-2x ≥ 0
===> -2x ≥ -25
===> x ≤ (-25)/(-2)
===> x ≤ 12,5.
Comme x ≥ 0, nous déduisons que : 0 ≤ x ≤ 12,5
Df = [0 ; 12,5]
Le volume d'un parallélépipède rectangle est donné par : Aire de la base * hauteur.
Prenons le carré comme base. Son aire est égale à x*x = x².
La hauteur est alors égale à y.
D'où, f(x) = x²y
Or y = 25-2x. (voir ci-dessus)
Donc [tex]f(x)=x^2(25-2x)[/tex] ou encore [tex]f(x)=25x^2 - 2x^3 [/tex]
3) Le graphique montre que f est maximal pour x ≈ 8,3 (cm)
(Graphique en pièce jointe)
Revenez nous voir pour des réponses mises à jour et fiables. Nous sommes toujours prêts à vous aider avec vos besoins en information. Nous espérons que nos réponses vous ont été utiles. Revenez quand vous voulez pour obtenir plus d'informations et de réponses à d'autres questions. Laurentvidal.fr est là pour vos questions. N'oubliez pas de revenir pour obtenir de nouvelles réponses.